10. Implied Volatilities and Model Calibration¶
This setion of the documentation illustrates how to calculate implied volatilities and how to calibrate a model to VSTOXX volatility index call option quotes. The example implements the calibration for a total of one month worth of data.
[1]:
from dx import *
import numpy as np
import pandas as pd
from pylab import plt
plt.style.use('seaborn')
10.1. VSTOXX Futures & Options Data¶
We start by loading VSTOXX data from a pandas HDFStore into DataFrame objects (source: Eurex, cf. http://www.eurexchange.com/advanced-services/).
[2]:
h5 = pd.HDFStore('./data/vstoxx_march_2014.h5', 'r')
vstoxx_index = h5['vstoxx_index']
vstoxx_futures = h5['vstoxx_futures']
vstoxx_options = h5['vstoxx_options']
h5.close()
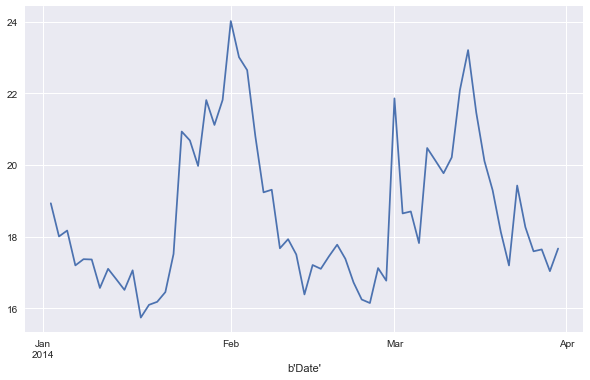
VSTOXX index for the first quarter of 2014.
[3]:
%matplotlib inline
vstoxx_index['V2TX'].plot(figsize=(10, 6))
[3]:
<matplotlib.axes._subplots.AxesSubplot at 0x115520978>
The VSTOXX futures data (8 futures maturities/quotes per day).
[4]:
vstoxx_futures.info()
<class 'pandas.core.frame.DataFrame'>
Int64Index: 504 entries, 0 to 503
Data columns (total 5 columns):
DATE 504 non-null datetime64[ns]
EXP_YEAR 504 non-null int64
EXP_MONTH 504 non-null int64
PRICE 504 non-null float64
MATURITY 504 non-null datetime64[ns]
dtypes: datetime64[ns](2), float64(1), int64(2)
memory usage: 23.6 KB
[5]:
vstoxx_futures.tail()
[5]:
| DATE | EXP_YEAR | EXP_MONTH | PRICE | MATURITY | |
|---|---|---|---|---|---|
| 499 | 2014-03-31 | 2014 | 7 | 20.40 | 2014-07-18 |
| 500 | 2014-03-31 | 2014 | 8 | 20.70 | 2014-08-15 |
| 501 | 2014-03-31 | 2014 | 9 | 20.95 | 2014-09-19 |
| 502 | 2014-03-31 | 2014 | 10 | 21.05 | 2014-10-17 |
| 503 | 2014-03-31 | 2014 | 11 | 21.25 | 2014-11-21 |
The VSTOXX options data. This data set is quite large due to the large number of European put and call options on the VSTOXX.
[6]:
vstoxx_options.info()
<class 'pandas.core.frame.DataFrame'>
Int64Index: 46960 entries, 0 to 46959
Data columns (total 7 columns):
DATE 46960 non-null datetime64[ns]
EXP_YEAR 46960 non-null int64
EXP_MONTH 46960 non-null int64
TYPE 46960 non-null object
STRIKE 46960 non-null float64
PRICE 46960 non-null float64
MATURITY 46960 non-null datetime64[ns]
dtypes: datetime64[ns](2), float64(2), int64(2), object(1)
memory usage: 2.9+ MB
[7]:
vstoxx_options.tail()
[7]:
| DATE | EXP_YEAR | EXP_MONTH | TYPE | STRIKE | PRICE | MATURITY | |
|---|---|---|---|---|---|---|---|
| 46955 | 2014-03-31 | 2014 | 11 | P | 85.0 | 63.65 | 2014-11-21 |
| 46956 | 2014-03-31 | 2014 | 11 | P | 90.0 | 68.65 | 2014-11-21 |
| 46957 | 2014-03-31 | 2014 | 11 | P | 95.0 | 73.65 | 2014-11-21 |
| 46958 | 2014-03-31 | 2014 | 11 | P | 100.0 | 78.65 | 2014-11-21 |
| 46959 | 2014-03-31 | 2014 | 11 | P | 105.0 | 83.65 | 2014-11-21 |
As a helper function we need a function to calculate all relevant third Fridays for all relevant maturity months of the data sets.
[8]:
import datetime as dt
import calendar
def third_friday(date):
day = 21 - (calendar.weekday(date.year, date.month, 1) + 2) % 7
return dt.datetime(date.year, date.month, day)
[9]:
third_fridays = {}
for month in set(vstoxx_futures['EXP_MONTH']):
third_fridays[month] = third_friday(dt.datetime(2014, month, 1))
[10]:
third_fridays
[10]:
{1: datetime.datetime(2014, 1, 17, 0, 0),
2: datetime.datetime(2014, 2, 21, 0, 0),
3: datetime.datetime(2014, 3, 21, 0, 0),
4: datetime.datetime(2014, 4, 18, 0, 0),
5: datetime.datetime(2014, 5, 16, 0, 0),
6: datetime.datetime(2014, 6, 20, 0, 0),
7: datetime.datetime(2014, 7, 18, 0, 0),
8: datetime.datetime(2014, 8, 15, 0, 0),
9: datetime.datetime(2014, 9, 19, 0, 0),
10: datetime.datetime(2014, 10, 17, 0, 0),
11: datetime.datetime(2014, 11, 21, 0, 0)}
10.2. Implied Volatilities from Market Quotes¶
Often calibration efforts are undertaken to replicate the market implied volatilities or the so-called volatility surface as good as possible. With DX Analytics and the BSM_european_option class, you can efficiently calculate (i.e. numerically estimate) implied volatilities. For the example, we use the VSTOXX futures and call options data from 31. March 2014.
Some definitions, the pre-selection of option data and the pre-definition of the market environment needed.
[11]:
V0 = 17.6639 # VSTOXX level on 31.03.2014
futures_data = vstoxx_futures[vstoxx_futures.DATE == '2014/3/31'].copy()
options_data = vstoxx_options[(vstoxx_options.DATE == '2014/3/31')
& (vstoxx_options.TYPE == 'C')].copy()
me = market_environment('me', dt.datetime(2014, 3, 31))
me.add_constant('initial_value', 17.6639) # index on 31.03.2014
me.add_constant('volatility', 2.0) # for initialization
me.add_curve('discount_curve', constant_short_rate('r', 0.01)) # assumption
options_data['IMP_VOL'] = 0.0 # initialization new iv column
The following loop now calculates the implied volatilities for all those options whose strike lies within the defined tolerance level.
[12]:
%%time
tol = 0.3 # tolerance level for moneyness
for option in options_data.index:
# iterating over all option quotes
forward = futures_data[futures_data['MATURITY'] == \
options_data.loc[option]['MATURITY']]['PRICE'].values
# picking the right futures value
if (forward * (1 - tol) < options_data.loc[option]['STRIKE']
< forward * (1 + tol)):
# only for options with moneyness within tolerance
call = options_data.loc[option]
me.add_constant('strike', call['STRIKE'])
me.add_constant('maturity', call['MATURITY'])
call_option = BSM_european_option('call', me)
options_data.loc[option, 'IMP_VOL'] = \
call_option.imp_vol(call['PRICE'], 'call', volatility_est=0.6)
CPU times: user 691 ms, sys: 6.05 ms, total: 698 ms
Wall time: 695 ms
A selection of the results.
[13]:
options_data[60:70]
[13]:
| DATE | EXP_YEAR | EXP_MONTH | TYPE | STRIKE | PRICE | MATURITY | IMP_VOL | |
|---|---|---|---|---|---|---|---|---|
| 46230 | 2014-03-31 | 2014 | 5 | C | 12.0 | 7.55 | 2014-05-16 | 0.000000 |
| 46231 | 2014-03-31 | 2014 | 5 | C | 13.0 | 6.55 | 2014-05-16 | 0.000000 |
| 46232 | 2014-03-31 | 2014 | 5 | C | 14.0 | 5.55 | 2014-05-16 | 1.541568 |
| 46233 | 2014-03-31 | 2014 | 5 | C | 15.0 | 4.55 | 2014-05-16 | 1.321803 |
| 46234 | 2014-03-31 | 2014 | 5 | C | 16.0 | 3.65 | 2014-05-16 | 1.153001 |
| 46235 | 2014-03-31 | 2014 | 5 | C | 17.0 | 2.90 | 2014-05-16 | 1.042549 |
| 46236 | 2014-03-31 | 2014 | 5 | C | 18.0 | 2.35 | 2014-05-16 | 0.997178 |
| 46237 | 2014-03-31 | 2014 | 5 | C | 19.0 | 1.90 | 2014-05-16 | 0.969301 |
| 46238 | 2014-03-31 | 2014 | 5 | C | 20.0 | 1.55 | 2014-05-16 | 0.958777 |
| 46239 | 2014-03-31 | 2014 | 5 | C | 21.0 | 1.30 | 2014-05-16 | 0.968430 |
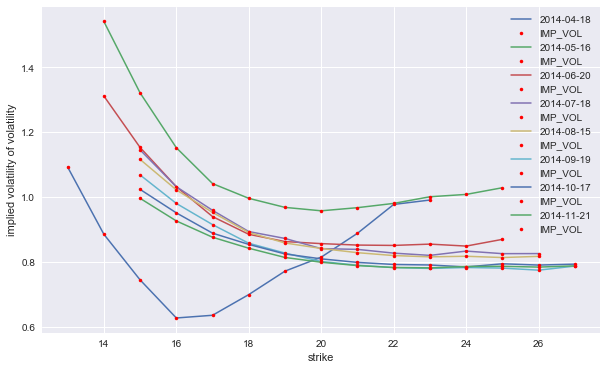
And the complete results visualized.
[14]:
import matplotlib.pyplot as plt
%matplotlib inline
plot_data = options_data[options_data.IMP_VOL > 0]
plt.figure(figsize=(10, 6))
for maturity in sorted(set(options_data['MATURITY'])):
data = plot_data.isin({'MATURITY': [maturity,]})
data = plot_data[plot_data.MATURITY == maturity]
# select data for this maturity
plt.plot(data['STRIKE'], data['IMP_VOL'],
label=maturity.date(), lw=1.5)
plt.plot(data['STRIKE'], data['IMP_VOL'], 'r.')
plt.xlabel('strike')
plt.ylabel('implied volatility of volatility')
plt.legend()
plt.show()
10.3. Market Modeling¶
This sub-section now implements the model calibration based on selected options data. In particular, we choose, for a given pricing date, the following options data:
- for a single maturity only
- call options only
- for a certain moneyness of the options
10.3.1. Relevant Market Data¶
The following following returns the relevant market data per calibration date:
[15]:
tol = 0.2
def get_option_selection(pricing_date, maturity, tol=tol):
''' Function selects relevant options data. '''
forward = vstoxx_futures[(vstoxx_futures.DATE == pricing_date)
& (vstoxx_futures.MATURITY == maturity)]['PRICE'].values[0]
option_selection = \
vstoxx_options[(vstoxx_options.DATE == pricing_date)
& (vstoxx_options.MATURITY == maturity)
& (vstoxx_options.TYPE == 'C')
& (vstoxx_options.STRIKE > (1 - tol) * forward)
& (vstoxx_options.STRIKE < (1 + tol) * forward)]
return option_selection, forward
10.3.2. Options Modeling¶
Given the options and their respective quotes to which to calibrate the model, the function get_option_models returns the DX Analytics option models for all relevant options. As risk factor model we use the square_root_diffusion class.
[16]:
def get_option_models(pricing_date, maturity, option_selection):
''' Models and returns traded options for given option_selection object. '''
me_vstoxx = market_environment('me_vstoxx', pricing_date)
initial_value = vstoxx_index['V2TX'][pricing_date]
me_vstoxx.add_constant('initial_value', initial_value)
me_vstoxx.add_constant('final_date', maturity)
me_vstoxx.add_constant('currency', 'EUR')
me_vstoxx.add_constant('frequency', 'W')
me_vstoxx.add_constant('paths', 10000)
csr = constant_short_rate('csr', 0.01)
# somewhat arbitrarily chosen here
me_vstoxx.add_curve('discount_curve', csr)
# parameters to be calibrated later
me_vstoxx.add_constant('kappa', 1.0)
me_vstoxx.add_constant('theta', 1.2 * initial_value)
me_vstoxx.add_constant('volatility', 1.0)
vstoxx_model = square_root_diffusion('vstoxx_model', me_vstoxx)
# square-root diffusion for volatility modeling
# mean-reverting, positive process
# option parameters and payoff
me_vstoxx.add_constant('maturity', maturity)
payoff_func = 'np.maximum(maturity_value - strike, 0)'
option_models = {}
for option in option_selection.index:
strike = option_selection['STRIKE'].ix[option]
me_vstoxx.add_constant('strike', strike)
option_models[option] = \
valuation_mcs_european_single(
'eur_call_%d' % strike,
vstoxx_model,
me_vstoxx,
payoff_func)
return vstoxx_model, option_models
The function calculate_model_values estimates and returns model value estimates for all relevant options given a parameter set for the square_root_diffusion risk factor model.
[17]:
def calculate_model_values(p0):
''' Returns all relevant option values.
Parameters
===========
p0 : tuple/list
tuple of kappa, theta, volatility
Returns
=======
model_values : dict
dictionary with model values
'''
kappa, theta, volatility = p0
vstoxx_model.update(kappa=kappa,
theta=theta,
volatility=volatility)
model_values = {}
for option in option_models:
model_values[option] = \
option_models[option].present_value(fixed_seed=True)
return model_values
10.4. Calibration Functions¶
10.4.1. Mean-Squared Error Calculation¶
The calibration of the pricing model is based on the minimization of the mean-squared error (MSE) of the model values vs. the market quotes. The MSE calculation is implemented by the function mean_squared_error which also penalizes economically implausible parameter values.
[18]:
i = 0
def mean_squared_error(p0):
''' Returns the mean-squared error given
the model and market values.
Parameters
===========
p0 : tuple/list
tuple of kappa, theta, volatility
Returns
=======
MSE : float
mean-squared error
'''
if p0[0] < 0 or p0[1] < 5. or p0[2] < 0 or p0[2] > 10.:
return 100
global i, option_selection, vstoxx_model, option_models, first, last
pd = dt.datetime.strftime(
option_selection['DATE'].iloc[0].to_pydatetime(),
'%d-%b-%Y')
mat = dt.datetime.strftime(
option_selection['MATURITY'].iloc[0].to_pydatetime(),
'%d-%b-%Y')
model_values = calculate_model_values(p0)
option_diffs = {}
for option in model_values:
option_diffs[option] = (model_values[option]
- option_selection['PRICE'].loc[option])
MSE = np.sum(np.array(list(option_diffs.values())) ** 2) / len(option_diffs)
if i % 150 == 0:
# output every 0th and 100th iteration
if i == 0:
print('%12s %13s %4s %6s %6s %6s --> %6s' % \
('pricing_date', 'maturity_date', 'i', 'kappa',
'theta', 'vola', 'MSE'))
print('%12s %13s %4d %6.3f %6.3f %6.3f --> %6.3f' % \
(pd, mat, i, p0[0], p0[1], p0[2], MSE))
i += 1
return MSE
10.4.2. Implementing the Calibration Procedure¶
The function get_parameter_series calibrates the model to the market data for every date contained in the pricing_date_list object for all maturities contained in the maturity_list object.
[19]:
import scipy.optimize as spo
def get_parameter_series(pricing_date_list, maturity_list):
global i, option_selection, vstoxx_model, option_models, first, last
# collects optimization results for later use (eg. visualization)
parameters = pd.DataFrame()
for maturity in maturity_list:
first = True
for pricing_date in pricing_date_list:
option_selection, forward = \
get_option_selection(pricing_date, maturity)
vstoxx_model, option_models = \
get_option_models(pricing_date, maturity, option_selection)
if first is True:
# use brute force for the first run
i = 0
opt = spo.brute(mean_squared_error,
((0.5, 2.51, 1.), # range for kappa
(10., 20.1, 5.), # range for theta
(0.5, 10.51, 5.0)), # range for volatility
finish=None)
i = 0
opt = spo.fmin(mean_squared_error, opt,
maxiter=200, maxfun=350, xtol=0.0000001, ftol=0.0000001)
parameters = parameters.append(
pd.DataFrame(
{'pricing_date' : pricing_date,
'maturity' : maturity,
'initial_value' : vstoxx_model.initial_value,
'kappa' : opt[0],
'theta' : opt[1],
'sigma' : opt[2],
'MSE' : mean_squared_error(opt)}, index=[0,]),
ignore_index=True)
first = False
last = opt
return parameters
10.4.3. The Calibration Itself¶
This completes the set of necessary function to implement such a larger calibration effort. The following code defines the dates for which a calibration shall be conducted and for which maturities the calibration is required.
[20]:
%%time
pricing_date_list = pd.date_range('2014/3/1', '2014/3/31', freq='B')
maturity_list = [third_fridays[7]]
parameters = get_parameter_series(pricing_date_list, maturity_list)
pricing_date maturity_date i kappa theta vola --> MSE
03-Mar-2014 18-Jul-2014 0 0.500 10.000 0.500 --> 4.507
pricing_date maturity_date i kappa theta vola --> MSE
03-Mar-2014 18-Jul-2014 0 2.500 15.000 5.500 --> 0.022
03-Mar-2014 18-Jul-2014 150 2.490 17.012 4.665 --> 0.005
Optimization terminated successfully.
Current function value: 0.004840
Iterations: 146
Function evaluations: 296
pricing_date maturity_date i kappa theta vola --> MSE
04-Mar-2014 18-Jul-2014 0 2.497 17.010 4.674 --> 0.048
04-Mar-2014 18-Jul-2014 150 2.474 17.633 4.738 --> 0.003
Optimization terminated successfully.
Current function value: 0.002750
Iterations: 70
Function evaluations: 164
pricing_date maturity_date i kappa theta vola --> MSE
05-Mar-2014 18-Jul-2014 0 2.474 17.633 4.738 --> 0.008
05-Mar-2014 18-Jul-2014 150 3.042 17.856 4.919 --> 0.003
05-Mar-2014 18-Jul-2014 300 4.407 17.995 5.667 --> 0.003
Warning: Maximum number of function evaluations has been exceeded.
pricing_date maturity_date i kappa theta vola --> MSE
06-Mar-2014 18-Jul-2014 0 4.407 17.995 5.668 --> 0.004
06-Mar-2014 18-Jul-2014 150 4.543 18.209 5.661 --> 0.003
Optimization terminated successfully.
Current function value: 0.003179
Iterations: 76
Function evaluations: 175
pricing_date maturity_date i kappa theta vola --> MSE
07-Mar-2014 18-Jul-2014 0 4.543 18.209 5.661 --> 0.030
07-Mar-2014 18-Jul-2014 150 4.958 18.332 5.553 --> 0.005
Optimization terminated successfully.
Current function value: 0.004775
Iterations: 84
Function evaluations: 183
pricing_date maturity_date i kappa theta vola --> MSE
10-Mar-2014 18-Jul-2014 0 4.958 18.332 5.553 --> 0.086
10-Mar-2014 18-Jul-2014 150 4.816 18.733 5.722 --> 0.003
Optimization terminated successfully.
Current function value: 0.002975
Iterations: 75
Function evaluations: 173
pricing_date maturity_date i kappa theta vola --> MSE
11-Mar-2014 18-Jul-2014 0 4.816 18.733 5.722 --> 0.006
11-Mar-2014 18-Jul-2014 150 4.281 19.060 5.162 --> 0.004
Optimization terminated successfully.
Current function value: 0.004069
Iterations: 100
Function evaluations: 210
pricing_date maturity_date i kappa theta vola --> MSE
12-Mar-2014 18-Jul-2014 0 4.281 19.060 5.162 --> 0.008
12-Mar-2014 18-Jul-2014 150 4.461 18.959 5.231 --> 0.005
Optimization terminated successfully.
Current function value: 0.004915
Iterations: 67
Function evaluations: 164
pricing_date maturity_date i kappa theta vola --> MSE
13-Mar-2014 18-Jul-2014 0 4.461 18.959 5.231 --> 0.007
13-Mar-2014 18-Jul-2014 150 4.515 18.920 5.333 --> 0.006
Optimization terminated successfully.
Current function value: 0.005971
Iterations: 84
Function evaluations: 189
pricing_date maturity_date i kappa theta vola --> MSE
14-Mar-2014 18-Jul-2014 0 4.515 18.920 5.333 --> 0.017
14-Mar-2014 18-Jul-2014 150 5.124 18.963 5.952 --> 0.003
Optimization terminated successfully.
Current function value: 0.002936
Iterations: 131
Function evaluations: 280
pricing_date maturity_date i kappa theta vola --> MSE
17-Mar-2014 18-Jul-2014 0 5.223 19.002 5.997 --> 0.025
17-Mar-2014 18-Jul-2014 150 5.330 18.581 6.097 --> 0.004
Optimization terminated successfully.
Current function value: 0.003809
Iterations: 81
Function evaluations: 185
pricing_date maturity_date i kappa theta vola --> MSE
18-Mar-2014 18-Jul-2014 0 5.330 18.581 6.097 --> 0.006
18-Mar-2014 18-Jul-2014 150 3.838 18.503 5.161 --> 0.003
Optimization terminated successfully.
Current function value: 0.002652
Iterations: 144
Function evaluations: 300
18-Mar-2014 18-Jul-2014 300 3.191 18.288 4.852 --> 0.003
pricing_date maturity_date i kappa theta vola --> MSE
19-Mar-2014 18-Jul-2014 0 3.191 18.288 4.852 --> 0.005
19-Mar-2014 18-Jul-2014 150 3.136 18.084 4.968 --> 0.003
Optimization terminated successfully.
Current function value: 0.003397
Iterations: 67
Function evaluations: 169
pricing_date maturity_date i kappa theta vola --> MSE
20-Mar-2014 18-Jul-2014 0 3.136 18.084 4.968 --> 0.010
20-Mar-2014 18-Jul-2014 150 2.936 18.441 4.849 --> 0.002
Optimization terminated successfully.
Current function value: 0.002263
Iterations: 128
Function evaluations: 267
pricing_date maturity_date i kappa theta vola --> MSE
21-Mar-2014 18-Jul-2014 0 2.928 18.450 4.842 --> 0.044
21-Mar-2014 18-Jul-2014 150 2.935 19.134 4.876 --> 0.004
Optimization terminated successfully.
Current function value: 0.003655
Iterations: 64
Function evaluations: 158
pricing_date maturity_date i kappa theta vola --> MSE
24-Mar-2014 18-Jul-2014 0 2.935 19.134 4.876 --> 0.021
24-Mar-2014 18-Jul-2014 150 5.169 18.555 6.217 --> 0.004
Optimization terminated successfully.
Current function value: 0.004381
Iterations: 138
Function evaluations: 297
pricing_date maturity_date i kappa theta vola --> MSE
25-Mar-2014 18-Jul-2014 0 5.653 18.592 6.449 --> 0.014
25-Mar-2014 18-Jul-2014 150 6.252 18.525 6.554 --> 0.003
Optimization terminated successfully.
Current function value: 0.002918
Iterations: 107
Function evaluations: 231
pricing_date maturity_date i kappa theta vola --> MSE
26-Mar-2014 18-Jul-2014 0 6.251 18.525 6.553 --> 0.014
26-Mar-2014 18-Jul-2014 150 5.189 18.301 6.063 --> 0.003
Optimization terminated successfully.
Current function value: 0.002839
Iterations: 107
Function evaluations: 243
pricing_date maturity_date i kappa theta vola --> MSE
27-Mar-2014 18-Jul-2014 0 5.189 18.301 6.063 --> 0.006
27-Mar-2014 18-Jul-2014 150 5.789 18.693 6.112 --> 0.003
Optimization terminated successfully.
Current function value: 0.002992
Iterations: 112
Function evaluations: 248
pricing_date maturity_date i kappa theta vola --> MSE
28-Mar-2014 18-Jul-2014 0 5.788 18.693 6.111 --> 0.003
28-Mar-2014 18-Jul-2014 150 5.684 18.828 5.974 --> 0.003
Optimization terminated successfully.
Current function value: 0.002811
Iterations: 97
Function evaluations: 216
pricing_date maturity_date i kappa theta vola --> MSE
31-Mar-2014 18-Jul-2014 0 5.683 18.828 5.974 --> 0.009
31-Mar-2014 18-Jul-2014 150 12.121 18.656 8.053 --> 0.004
31-Mar-2014 18-Jul-2014 300 15.247 18.578 8.978 --> 0.004
Warning: Maximum number of function evaluations has been exceeded.
CPU times: user 1min 6s, sys: 278 ms, total: 1min 6s
Wall time: 1min 6s
10.5. Calibration Results¶
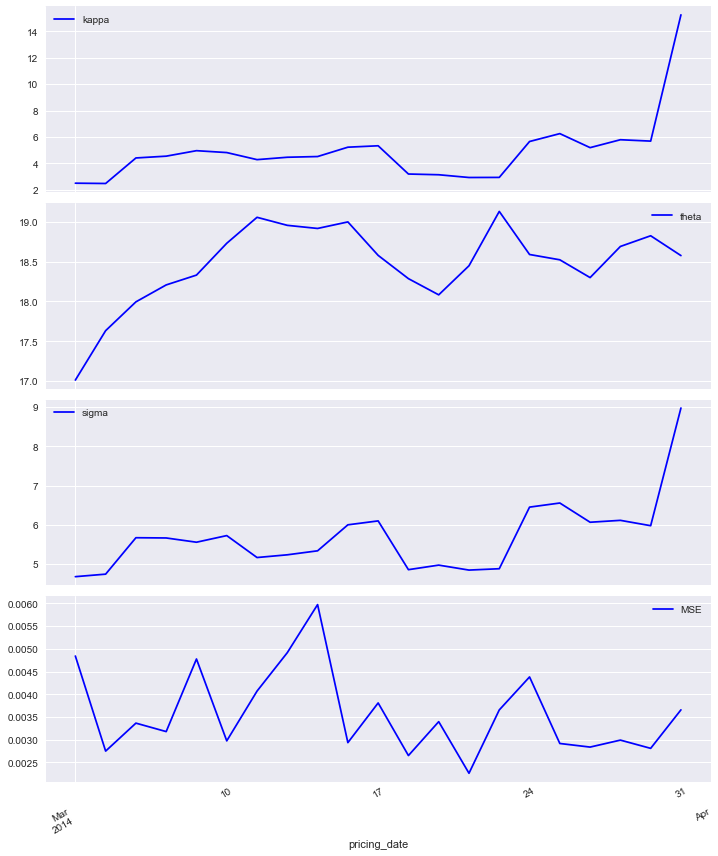
The results are now stored in the pandas DataFrame called parameters. We set a new index and inspect the last results. Throughout the MSE is pretty low indicated a good fit of the model to the market quotes.
[21]:
paramet = parameters.set_index('pricing_date')
paramet.tail()
[21]:
| MSE | initial_value | kappa | maturity | sigma | theta | |
|---|---|---|---|---|---|---|
| pricing_date | ||||||
| 2014-03-25 | 0.002918 | 18.2637 | 6.250875 | 2014-07-18 | 6.553352 | 18.525022 |
| 2014-03-26 | 0.002839 | 17.5869 | 5.189260 | 2014-07-18 | 6.062754 | 18.301087 |
| 2014-03-27 | 0.002992 | 17.6397 | 5.787693 | 2014-07-18 | 6.111093 | 18.693053 |
| 2014-03-28 | 0.002811 | 17.0324 | 5.683422 | 2014-07-18 | 5.974289 | 18.827773 |
| 2014-03-31 | 0.003657 | 17.6639 | 15.246458 | 2014-07-18 | 8.978325 | 18.578233 |
This is also illustrated by the visualization of the time series data for the calibrated/optimal parameter values. The MSE is below 0.01 throughout.
[22]:
%matplotlib inline
paramet[['kappa', 'theta', 'sigma', 'MSE']].plot(subplots=True, color='b', figsize=(10, 12))
plt.tight_layout()
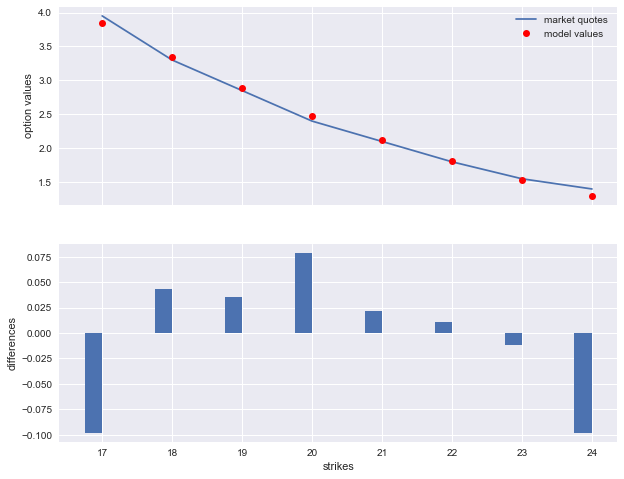
The following generates a plot of the calibration results for the last calibration day. The absolute price differences are below 0.10 EUR for all options.
[23]:
index = paramet.index[-1]
opt = np.array(paramet[['kappa', 'theta', 'sigma']].loc[index])
option_selection = get_option_selection(index, maturity_list[0], tol=tol)[0]
model_values = np.sort(np.array(list(calculate_model_values(opt).values())))[::-1]
import matplotlib.pyplot as plt
%matplotlib inline
fix, (ax1, ax2) = plt.subplots(2, sharex=True, figsize=(10, 8))
strikes = option_selection['STRIKE'].values
ax1.plot(strikes, option_selection['PRICE'], label='market quotes')
ax1.plot(strikes, model_values, 'ro', label='model values')
ax1.set_ylabel('option values')
ax1.grid(True)
ax1.legend(loc=0)
wi = 0.25
ax2.bar(strikes - wi / 2., model_values - option_selection['PRICE'],
label='market quotes', width=wi)
ax2.grid(True)
ax2.set_ylabel('differences')
ax2.set_xlabel('strikes')
[23]:
<matplotlib.text.Text at 0x116ec0b00>
Copyright, License & Disclaimer
© Dr. Yves J. Hilpisch | The Python Quants GmbH
DX Analytics (the “dx library” or “dx package”) is licensed under the GNU Affero General Public License version 3 or later (see http://www.gnu.org/licenses/).
DX Analytics comes with no representations or warranties, to the extent permitted by applicable law.
http://tpq.io | dx@tpq.io | http://twitter.com/dyjh
Quant Platform | http://pqp.io
Python for Finance Training | http://training.tpq.io
Certificate in Computational Finance | http://compfinance.tpq.io
Derivatives Analytics with Python (Wiley Finance) | http://dawp.tpq.io
Python for Finance (2nd ed., O’Reilly) | http://py4fi.tpq.io
